カメラ座標系とワールド座標系の変換

OpenCVのDocumentationにある，ワールド座標系とカメラ座標系の間の変換

(1)[xyz]=R[XYZ]+t

はぱっと見ただけではわかりづらいので，ワールド座標系とカメラ座標系をしっかりと定め，その間の変換(式 (1) )を導出します．

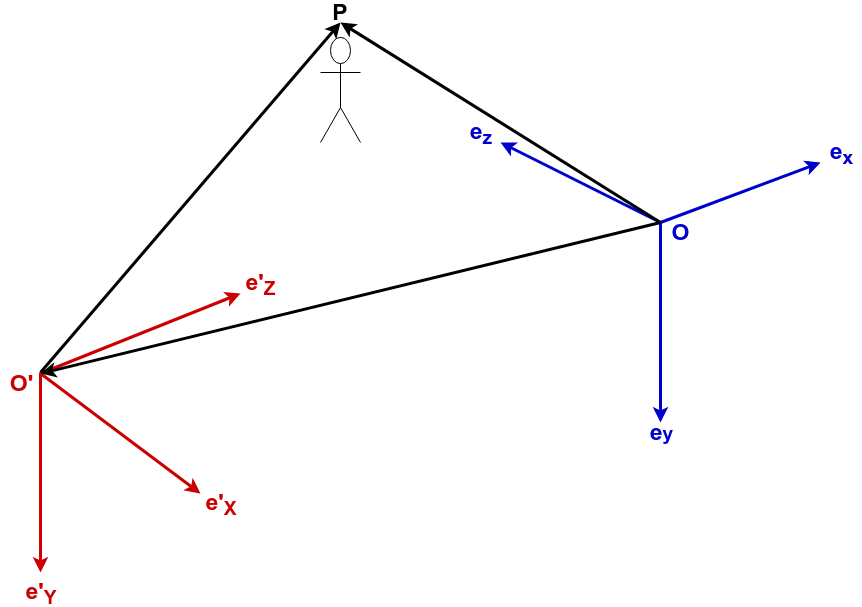
ここでは原点 O ，基底 ex, ey, ez から成る直交座標系を O[ex,ey,ez] と表記することにします．

また，ワールド座標系とカメラ座標系をそれぞれ次のように設定します．

原点を O’ としたときのワールド座標系	O′[e′X,e′Y,e′Z]
位置 O のカメラの座標系	O[ex,ey,ez]

カメラに映っている物体の座標を P とし，これをそれぞれの座標系で表現すると

→O′P=Xe′X+Ye′Y+Ze′Z=[e′Xe′Ye′Z][XYZ]→OP=xex+yey+zez=[exeyez][xyz]

となります．

ベクトル →OO′ をカメラ座標系 O[ex,ey,ez] で表現すると

→OO′=txex+tyey+tzez=[exeyez][txtytz]

また， →OP=→OO′+→O′P より，

(2)[exeyez][xyz]=[e′Xe′Ye′Z][XYZ]+[exeyez][txtytz]

と書けます．

ワールド座標系 O′[e′X,e′Y,e′Z] とカメラ座標系 O[ex,ey,ez] はそれぞれ別々の座標系ではあるものの，どちらも同じ3次元空間に共存しており，かつ直交座標系であるため，片方の基底を用いてもう片方の基底を表現することができます．

この変換を回転行列 R∈R3×3 を用いて

[e′Xe′Ye′Z]=[exeyez]R

と表記すると，式 (2) は

[exeyez][xyz]=[exeyez]R[XYZ]+[exeyez][txtytz]

と書き換えることができます．

両辺から基底部分を取り除くと

[xyz]=R[XYZ]+[txtytz].

さらに

t=[txtytz]

とおけば，

[xyz]=R[XYZ]+t

というふうに座標変換を記述することができます．